Hopscotch hashing

This article presents an implementation of a single-threaded hash map using the hopscotch hashing technique.

Hopscotch hashing was introduced by Herlihy et al. 2008¹ and resolves collisions using open addressing (the records are stored in the bucket array itself and not through chaining). The algorithm presented in the paper is a multi-threaded hash map with a high throughput. Here we will focus on a single-thread implementation inspired by this paper.

The main idea behind the algorithm is the notion of neighborhood. Each bucket B has a neighborhood of size H, which is the bucket B and the H-1 buckets following it in the bucket array. When we are searching for a value, we will search it in its initial bucket and the neighborhood of the bucket. On insert, we will keep the inserted value in the neighborhood of its initial bucket through swapping.

We will describe how we proceed to insert, find and erase elements in the hash map.

The C++ implementation can be found on GitHub and there is a benchmark of the implementation here.

Overview

Insert

To insert an item x in the hash map, where hash(x) % nb_buckets = i, we need:

• From the bucket i, search for an empty bucket j through linear probing.
• If the bucket j is in the neighborhood of i (i.e. j - i < H), insert it there and we are done.
• Otherwise, find in the interval [j - H + 1, j), an item y where hash(y) % nb_buckets >= j - H. Swap the bucket for the item y with the empty bucket j and repeat until j is in the neighborhood of i.

Example

An example with images will be easier.

We have a bucket array of size 10 with 7 elements. The little number on the bottom right corner of each entry is the bucket where the item really belongs to (the i bucket, hash(item) % nb_buckets).

In this example, the size of the neighborhood (H) is equal to 3. For example the neighborhood of bucket 1 is composed of the buckets 1, 2 and 3.

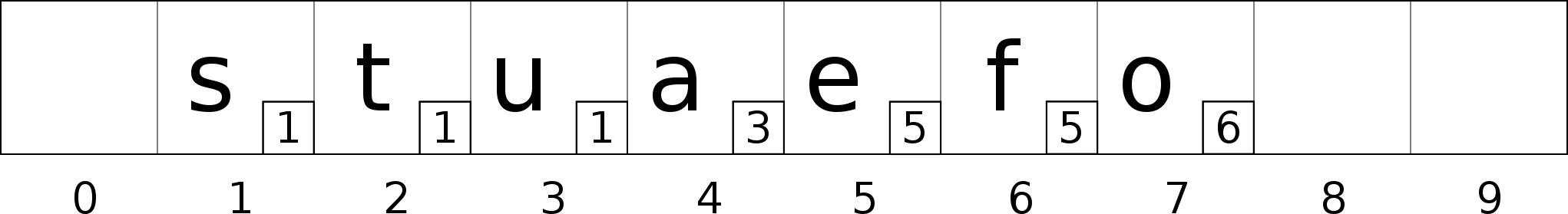
Let’s say we want to insert the item ‘d’ with hash(‘d’) % 10 = 2. From the bucket 2, we start to search for an empty bucket through linear probing.

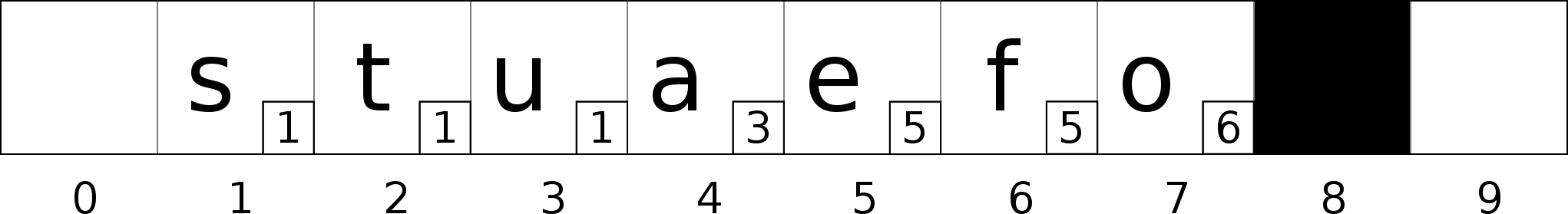
We found the bucket 8, but bucket 8 is not in the neighborhood of bucket 2 (8 - 2 >= H). We need to search for a bucket to swap.

The bucket 7 is a good candidate, the bucket 8 is in the neighborhood of the bucket 6 which is the bucket the value ‘o’ belongs to (8 - 6 < H). Swap bucket 7 with bucket 8.

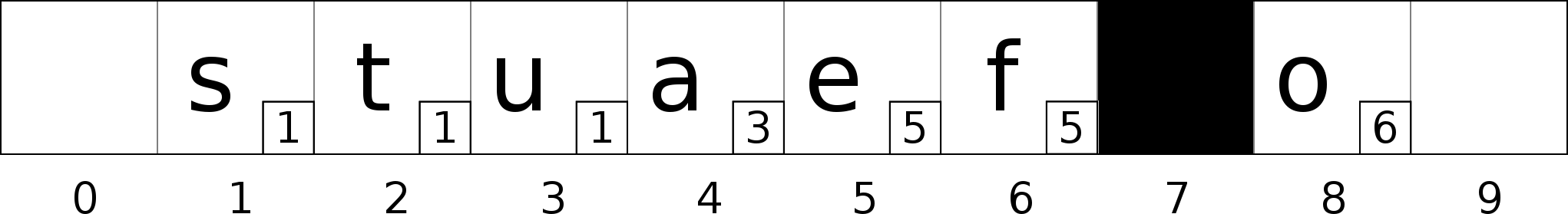
Bucket 7 is still not in the neighborhood of bucket 2. We need to continue the swapping process.

The bucket 5 is a good candidate, the bucket 7 is in the neighborhood of the bucket 5 which is the bucket the value ‘e’ belongs to (7 - 5 < H). Swap bucket 5 with bucket 7.

Bucket 5 is still not in the neighborhood of bucket 2. We need to continue the swapping process.

The bucket 4 is a good candidate, the bucket 5 is in the neighborhood of the bucket 3 which is the bucket the value ‘a’ belongs to (5 - 3 < H). Swap bucket 4 with bucket 5.

Bucket 4 is in the neighborhood of bucket 2 (4 - 2 < H), insert the value ‘d’ in bucket 4.

We are now good, the neighborhood constraint is still valid.

But what happen if there is no candidate for swapping or the neighborhood of the bucket is full (example bucket 1 has already H values belonging to it)? As the paper suggests, we resize the bucket array and we rehash, the modulo will be bigger and so the elements will end-up in different buckets.

Now this is all good but there is one thing still missing which the paper did not mention. What if we have more than H values for which the hash function returns the exact same hash? Resizing the bucket array will not change anything as they will still end-up to belong to the same bucket. Even if the modulo nb_buckets gets bigger, if hash(x) return the same value for different values of x, they will all belong to the same bucket. If the hash function is good and the neighborhood size is not too small, it should never really happen but it still may.

To solve the problem, a linked list was added in the implementation in addition to the bucket array. This linked list will contain overflow elements. If we can not insert the item in the neighborhood of its bucket, even through swapping and rehash, it will go into the overflow list and a tag will be added to the bucket to notify that some elements belonging to the bucket are in the overflow list.

This will dismiss our cache locality, but it should be really rare for elements to end-up in the overflow list.

Find

To find an element in the hash table, we just compute its bucket with hash(element) % nb_buckets. We then search in the bucket and its neighbors. If the bucket has been marked as overflow, we also do a linear search in the overflow list.

Erase

To erase, we just have to find the element and remove it, either from the bucket array or the overflow list. If the element was the last element of the bucket in the overflow list, we can also remove the overflow tag.

Implementation

The implementation is mainly composed of two structures, the bucket array and the overflow list.

The bucket array

The bucket array is a vector of hopscotch_bucket, std::vector<hopscotch_bucket>. Each hopscotch_bucket contains two members, a std::aligned_storage to store the key-value pair and an integer that is used as bitmap.

This bitmap serves multiple purposes:

• The least significant bit tells us if the bucket contains a value or not.
• The second least significant bit tells us if the bucket has some elements belonging to it in the overflow list.
• Then we have a number of bits of the size of the neighborhood (H). From the least significant to the most significant, it tells us which neighbors contain a value belonging to the bucket, going from the current bucket to the most far away neighbor.

The overflow list

The overflow list is just a std::list<std::pair<const Key, Value>>. When an element can not be stored in the bucket array, it will be pushed back into the list.

Conclusion

This algorithm offers good performances thanks to its cache locality. This advantage is only valid if the key doesn’t use some pointers to other parts of the memory to check its equality with another key. If it is the case, the algorithm will not be as efficient.

It also offers some upper-bound when we are searching for an element of NeighborhoodSize + |OverflowList| operations, where the size of OverflowList is usually equal to 0.

References